मैं Pythagoras Theorem (पाइथागोरस प्रमेय) के बारे में कहाँ पढ़ सकता हूँ?

इस पोस्ट में Pythagoras Theorem (पाइथागोरस प्रमेय) - परिभाषा, सूत्र और उदाहरण आदि सहित Pythagoras Theorem (पाइथागोरस प्रमेय) की सभी महत्वपूर्ण जानकारी दी हैं.

Pythagoras Theorem: पाइथागोरस प्रमेय – परिभाषा, सूत्र और उदाहरण

पाइथागोरस प्रमेय (Pythagoras Theorem)

पाइथागोरस प्रमेय (Pythagoras Theorem) गणित का एक महत्वपूर्ण सिद्धांत है, जो समकोण त्रिभुज (Right-angled triangle) से संबंधित है.

गणित में पाइथागोरस प्रमेय बहुत ही सामान्य और महत्वपूर्ण विषय. यह समकोण त्रिभुज के विभिन्न पक्षों के बीच के संबंध की व्याख्या करता है. प्रमेय बताता है कि “एक समकोण त्रिभुज में, कर्ण का वर्ग त्रिभुज के अन्य दो पक्षों के वर्गों के योग के बराबर होता है.”

प्रतियोगी परीक्षा के लिए क्यों है महत्वपूर्ण?

पाइथागोरस प्रमेय (Pythagoras Theorem) प्रतियोगी परीक्षाओं के लिए अत्यंत महत्वपूर्ण विषय है, खासकर उन परीक्षाओं में जहाँ गणित और तर्कशक्ति (Reasoning) से संबंधित प्रश्न पूछे जाते हैं, जैसे SSC, Railways, Banking, Defence, और अन्य सरकारी परीक्षाएँ। अगर अभ्यर्थी पाइथागोरस प्रमेय और इसके अनुप्रयोगों को अच्छी तरह समझ लें, तो वे त्रिभुजों, दूरी, क्षेत्रफल और ऊँचाई जैसे प्रश्नों को आसानी से हल कर सकते हैं।

प्रमेय क्या कहता है?

एक समकोण त्रिभुज में, कर्ण (सबसे लंबी भुजा) का वर्ग, अन्य दो भुजाओं (कर्ण को छोड़कर) के वर्गों के योग के बराबर होता है।

अन्य दो पक्ष यहाँ त्रिभुज के लंबवत और आधार हैं। इसलिए, एक समकोण त्रिभुज में, Hypotenuse इसका सबसे लंबा भाग बन जाता है, क्योंकि यह 90 ° कोण के सामने हैं.

PYTHAGOREAN THEOREM का FORMULA

एक समकोण त्रिभुज में,

A, लंबवत है

B आधार है

C कर्ण है

Therefore, according to the definition of the Pythagorean Theorem, the formula would be:

Hypotenuse²= Perpendicular² + Base²

In other words, it would be:

C²= A²+ B²

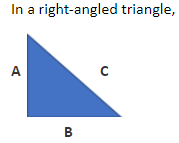
पाइथागोरस प्रमेय का PROOF :

समकोण त्रिभुज में, आधार और लम्ब एक-दूसरे के साथ 90 डिग्री का कोण बनाते हैं. इसलिए, पाइथागोरस प्रमेय के अनुसार, “कर्ण का वर्ग आधार के वर्ग और लंब के वर्ग के योग के बराबर है।”
“the square of the hypotenuse is equal to the sum of a base square and perpendicular square.”

इस प्रमेय को सिद्ध करने के लिए,

मान लें कि एक त्रिभुज ABC है, जिसका कोण B समकोण है.

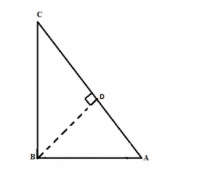
Pythagoras Theorem: पाइथागोरस प्रमेय – परिभाषा, सूत्र और उदाहरण | Latest Hindi Banking jobs_5.1

हमें सिद्ध करना है : AC²= AB² + BC²

To explain: हम एक सीधा रेखा BD खींचते हैं जो D पर AC से मिलती है.
Proof:

हम प्रमेय द्वारा जानते हैं कि यदि एक समकोण त्रिभुज के कर्ण से समकोण की ओर से खींचा जाता है, तो लम्बवत् के दोनों किनारों पर दो त्रिभुज एक दूसरे के समान होते हैं.

इसलिए,

△ADB ~ △ABC

Hence,

AD/AB = AB/AC (Condition for similarity)

Or, AB² = AD × AC (1)

Also, △BDC ~△ABC (By applying the same theorem)

Therefore,

CD/BC = BC/AC (Condition for similarity)

Or,

BC²= CD × AC (2)

Now,

By adding the equations (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.

पाइथागोरस प्रमेय के उदाहरण

पाइथागोरस प्रमेय का उपयोग विभिन्न प्रकार की समस्याओं को हल करने के लिए किया जा सकता है। आइए कुछ उदाहरणों के माध्यम से समझते हैं:

उदाहरण 1: एक सीढ़ी की लंबाई ज्ञात करना

मान लीजिए एक सीढ़ी एक दीवार के सहारे रखी हुई है। सीढ़ी का निचला सिरा दीवार से 3 मीटर की दूरी पर है और दीवार पर 4 मीटर की ऊंचाई तक पहुंचता है। सीढ़ी की लंबाई ज्ञात कीजिए।

हल:
- सीढ़ी, दीवार और जमीन मिलकर एक समकोण त्रिभुज बनाते हैं।
- सीढ़ी कर्ण है, दीवार लंब है और जमीन आधार है।
- पाइथागोरस प्रमेय के अनुसार, कर्ण² = लंब² + आधार²
- सीढ़ी² = 3² + 4²
- सीढ़ी² = 9 + 16
- सीढ़ी² = 25
- सीढ़ी = √25 = 5 मीटर

अतः, सीढ़ी की लंबाई 5 मीटर है।

उदाहरण 2: एक आयत के विकर्ण की लंबाई ज्ञात करना

मान लीजिए एक आयत की लंबाई 8 सेमी और चौड़ाई 6 सेमी है। आयत के विकर्ण की लंबाई ज्ञात कीजिए।

हल:
- आयत के विकर्ण, लंबाई और चौड़ाई मिलकर एक समकोण त्रिभुज बनाते हैं।
- विकर्ण कर्ण है, लंबाई लंब है और चौड़ाई आधार है।
- पाइथागोरस प्रमेय के अनुसार, विकर्ण² = लंब² + चौड़ाई²
- विकर्ण² = 8² + 6²
- विकर्ण² = 64 + 36
- विकर्ण² = 100
- विकर्ण = √100 = 10 सेमी

अतः, आयत का विकर्ण 10 सेमी लंबा है।

उदाहरण 3: एक वृत्त में खींचे गए जीवा की लंबाई ज्ञात करना

मान लीजिए एक वृत्त की त्रिज्या 5 सेमी है और वृत्त के केंद्र से जीवा की दूरी 3 सेमी है। जीवा की लंबाई ज्ञात कीजिए।

हल:
- वृत्त का केंद्र, जीवा का मध्यबिंदु और वृत्त पर जीवा का एक सिरा मिलकर एक समकोण त्रिभुज बनाते हैं।
- वृत्त की त्रिज्या कर्ण है, जीवा का आधा भाग लंब है और केंद्र से जीवा की दूरी आधार है।
- पाइथागोरस प्रमेय का उपयोग करके हम जीवा के आधे भाग की लंबाई ज्ञात कर सकते हैं और फिर इसे 2 से गुणा करके पूरी जीवा की लंबाई ज्ञात कर सकते हैं।

यह ध्यान रखना महत्वपूर्ण है कि पाइथागोरस प्रमेय का उपयोग केवल समकोण त्रिभुजों के लिए किया जा सकता है।

पाइथागोरस प्रमेय के उपयोग

त्रिभुज की भुजाओं की लंबाई ज्ञात करना: यदि हमें किसी समकोण त्रिभुज की दो भुजाओं की लंबाई पता हो, तो हम तीसरी भुजा की लंबाई इस प्रमेय का उपयोग करके ज्ञात कर सकते हैं।
दूरी ज्ञात करना: भूगोल, खगोल विज्ञान और इंजीनियरिंग में दूरी ज्ञात करने के लिए पाइथागोरस प्रमेय का व्यापक रूप से उपयोग किया जाता है।
तीन-आयामी ज्यामिति: तीन-आयामी ज्यामिति में भी पाइथागोरस प्रमेय का उपयोग किया जाता है।
भौतिकी: गति, बल और ऊर्जा से संबंधित कई भौतिकी की समस्याओं को हल करने के लिए पाइथागोरस प्रमेय का उपयोग किया जाता है।

Trigonometry: Formulas, Tricks and Questions

Number Series Questions for Bank Exams