दिए गए प्रश्नों में दो मात्राएँ,’मात्रा I’ और ‘मात्रा II’, दी गई हैं। आपको दो मात्राओं के बीच संबंध निर्धारित करना है और उपयुक्त विकल्प चुनना है:
Q1. एक व्यक्ति ने दो योजनाओं ‘A’ और ‘B’ में 8:11 के अनुपात में निवेश किया। योजना ‘A’ ने चक्रवृद्धि ब्याज प्रदान करती है, जबकि योजना ‘B’ ने साधारण ब्याज प्रदान करती है।
मात्रा I – योजना ‘B’ में निवेश की गई राशि।
यदि योजना ‘A’ और ‘B’ में दी जाने वाली ब्याज दर क्रमशः 20% प्रति वर्ष और 16% प्रति वर्ष थी और व्यक्ति को दो वर्षों के बाद दोनों योजनाओं से कुल ब्याज के रूप में 3520 रुपये मिले।
मात्रा II – योजना ‘A’ में व्यक्ति द्वारा निवेश की गई राशि।
यदि योजना ‘A’ और ‘B’ में दी जाने वाली ब्याज दर क्रमशः 10% प्रति वर्ष और 20% प्रति वर्ष थी और व्यक्ति को वर्षों के बाद ‘A’ की तुलना में योजना ‘B’ से ब्याज के रूप में 1870 रुपये अधिक मिले। (a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q2. एक बैग में 9 पीली गेंदें, Y हरी गेंदें और 7 लाल गेंदें हैं, यदि बैग से यादृच्छिक रूप से एक गेंद निकाली जाती है तो उसके हरे रंग की गेंद होने की प्रायिकता 5/21 है।
मात्रा I – प्रायिकता कि फलों में से कम से कम एक सेब है, जब बाल्टी P से दो फलों को बिना प्रतिस्थापन के निकाला जाता है।
बाल्टी ‘P’ में 2Y सेब, 3(Y – 2) केले और 1.5(Y – 1) संतरे हैं।
मात्रा II – प्रायिकता कि दोनों पासे एक ही रंग के हैं, जब बाल्टी Q में से दो पासे बिना प्रतिस्थापन के निकाले जाते हैं।
थैले ‘Q’ में 4 लाल पासे, 3.5(Y – 3) हरे पासे और 2Y पीले पासे हैं।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q3. दो बर्तन A और B में दूध और पानी का मिश्रण क्रमशः (X + 54) लीटर और (X + 84) लीटर की मात्रा में है। बर्तन A और बर्तन B में दूध और पानी का अनुपात क्रमशः 3:2 और 2:1 है।
मात्रा I – बर्तन B में दूध की मात्रा।
यदि बर्तन A से 60% मिश्रण और बर्तन B से 66 ⅔ % मिश्रण निकाल लिया जाए, तो दोनों बर्तनों में शेष मिश्रण बराबर है।
मात्रा II – 144 लीटर
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q4. मात्रा I – आयत की चौड़ाई।
एक वृत्त की परिधि और एक आयत के परिमाप का योग 154 सेमी और वृत्त का क्षेत्रफल 346.5 सेमी2 है। आयत की लंबाई वृत्त की त्रिज्या से 166 ⅔% अधिक है।
मात्रा II – वर्ग की भुजा।
एक वृत्त की परिधि 132 सेमी है और वृत्त का क्षेत्रफल वर्ग के क्षेत्रफल से 1130 सेमी2 अधिक है।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q5. मात्रा I – गोपाल द्वारा निवेश की गई राशि का तीन गुना।
अरुण और गोपाल ने क्रमशः (P + 1200) रुपये और (P + 1500) रुपये की पूंजी के साथ एक व्यवसाय में प्रवेश किया। शुरू होने के 8 महीने बाद, अरुण ने अपने निवेश का आधा हिस्सा वापस ले लिया और गोपाल ने अपने निवेश को दोगुना कर दिया। वर्ष के अंत में अरुण को 11250 रुपये के कुल लाभ में से 4250 रुपये मिले।
मात्रा II – C का लाभ हिस्सा।
A और B ने क्रमशः 27000 रुपये और 36000 रुपये के शुरुआती निवेश के साथ एक व्यवसाय शुरू किया। 4 महीने के बाद A ने 5000 रुपये निकाले, B ने 6000 रुपये जोड़े और C 35000 रुपये का निवेश करके उनके साथ जुड़ गया। एक साल के अंत में 130500 रुपये का कुल लाभ प्राप्त होता है।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Directions (6-10): नीचे दिया गया रेखा ग्राफ किलोमीटर में दिल्ली से पांच अलग-अलग शहरों के बीच की दूरी को दर्शाता है और नीचे दी गई तालिका किमी/घंटा में पांच अलग-अलग कारों की गति को दर्शाती है।
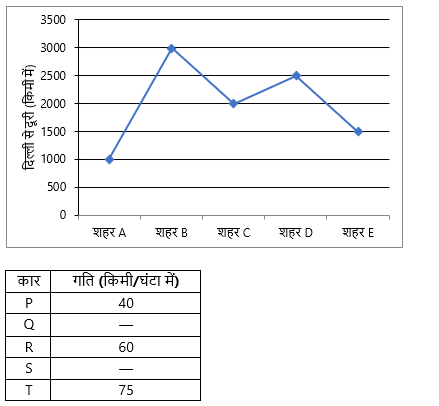
नोट: – कुछ डेटा लुप्त है, आपको प्रश्न के अनुसार गणना करनी होगी।
Q6. कार ‘P’ द्वारा शहर ‘E’ से दिल्ली और फिर दिल्ली से शहर ‘B’ तक जाने में लिया गया समय, कार ‘R’ द्वारा दिल्ली से शहर ‘A’ और फिर शहर ‘A’ से शहर ‘B’ तक जाने में लिए गए समय के बराबर है। शहर ‘A’ और शहर ‘B’ के बीच की दूरी ज्ञात कीजिए।
(a) 5650 किमी
(b) 5750 किमी
(c) 5450 किमी
(d) 5550 किमी
(e) 5320 किमी
Q7. शहर ‘A’ से शहर ‘E’ तक पहुंचने में कार ‘T’ का अनुमानित समय ज्ञात कीजिए, यदि शहर ‘A’ और शहर ‘E’ क्रमशः दिल्ली के उत्तर और पूर्व दिशा में हैं।
(a) 24 घंटे
(b) 27 घंटे
(c) 20 घंटे
(d) 36 घंटे
(e) 42 घंटे
Q8. कार Q और कार S क्रमशः शहर B और शहर C के लिए दिल्ली से शुरू होती हैं और वे समान समय में पहुँचती हैं। यदि कार Q और कार S क्रमशः शहर B और शहर D से एक ही समय पर चलना शुरू करते हैं और एक-दूसरे की ओर बढ़ते हैं, तो कार Q द्वारा कार S को पार करने में लिया गया समय, कार Q द्वारा दिल्ली से शहर B तक पहुंचने में लगने वाले समय का कितना प्रतिशत है। शहर B और शहर D के बीच की दूरी 1500 किमी है।
(a) 25%
(b) 20%
(c) 30%
(d) 40%
(e) 50%
Q9. एक चोर कार S में दिल्ली से शहर E की ओर बढ़ता है और 6 घंटे चलने के बाद, एक पुलिसकर्मी ने उसे एक कार R से पकड़ना शुरू किया। इससे चोर अपनी कार की गति 100% बढ़ा देता है। इससे पुलिसकर्मी उसे दिल्ली से शहर E की दूरी के 3/5 भाग पर पकड़ लेता है। कार ‘S’ की प्रारंभिक गति ज्ञात कीजिए।
(a) 15 किमी/घंटा
(b) 27 किमी/घंटा
(c) 20 किमी/घंटा
(d) 25 किमी/घंटा
(e) 40 किमी/घंटा
Q10. कार P और कार Q दिल्ली से शहर A के लिए चलना शुरू करते हैं। कार Q पहले शहर A तक पहुँचती है और रास्ते में कार P से मिलती है, जो शहर ‘A’ से 200 किमी दूर है। यदि वे आना-जाना जारी रखते हैं तो वे पहली बार मिलने के बाद दूसरी बार कितने समय बाद मिलेंगे।
(a) 24 घंटे
(b) 15 घंटे
(c) 16 घंटे
(d) 25 घंटे
(e) 20 घंटे
Solutions:
