LIC ADO Mains क्वांट क्विज 2023 – 16th April

Q1. निखिलेश ने तीन अलग-अलग योजनाओं A, B और C में क्रमशः 10 प्रतिशत प्रति वर्ष, 12 प्रतिशत प्रति वर्ष और 15 प्रतिशत प्रति वर्ष की दर से एक निश्चित राशि का निवेश किया। यदि एक वर्ष में अर्जित कुल ब्याज 3200 रुपये था और योजना C में निवेश की गई राशि योजना A में निवेश की गई राशि का 150% थी और योजना B में निवेश की गई राशि का 240% थी, तो योजना B में निवेश की गई राशि क्या थी?
(a) 8000 रुपये
(b) 5000 रुपये
(c) 6500 रुपये
(d) 12000 रुपये
(e) 10000 रुपये

Q2. A, B और C 3 : 4 : 5 के अनुपात में निवेश करते हैं। उनके निवेश पर प्रतिफल का प्रतिशत 6 : 5 : 4 के अनुपात में है। कुल कमाई ज्ञात कीजिए, यदि B, A से 250 रुपये अधिक कमाता है:
(a) 6000 रुपये
(b) 7250 रुपये
(c) 5000 रुपये
(d) 7000 रुपये
(e) 8000 रुपये

Q3. राजीव ने शेष महीने में अपनी औसत कमाई 600 रुपये प्रति माह की तुलना में जनवरी, अप्रैल, जुलाई और अक्टूबर में 3/2 गुना कमाता है। तो उसकी बाकी महीनों की बचत 400 रुपये प्रति माह की तुलना में जनवरी, अप्रैल, जुलाई और अक्टूबर की बचत 5/4 गुना हो जाती है। प्रति माह का औसत व्यय है:
(a) 266.67 रुपये
(b) 250 रुपये
(c) 233.33 रुपये
(d) 433.33 रुपये
(e) 245 रुपये

Q4. यदि एक व्यक्ति 5 किमी प्रति घंटे की गति से चलता है, तो उसकी एक ट्रेन 7 मिनट पहले छूट जाती है। हालाँकि, यदि वह 6 किमी प्रति घंटे की गति से चलता है, तो वह ट्रेन के आने से 5 मिनट पहले स्टेशन पहुँच जाता है। स्टेशन पहुँचने में उसके द्वारा तय की गई दूरी ज्ञात कीजिए।
(a) 4 किमी
(b) 6 किमी
(c) 5 किमी
(d) 7 किमी
(e) 9 किमी

Q5. विभाग A के 25% कर्मचारियों और विभाग B के 16% कर्मचारियों ने एक समारोह में भाग लिया। विभाग A के प्रतिभागियों की संख्या 500 थी लेकिन विभाग B के 252 कर्मचारियों ने समारोह में भाग नहीं लिया। A और B में कर्मचारियों की कुल संख्या ज्ञात कीजिए।
(a) 2200
(b) 2300
(c) 2000
(d) 2500
(e) 2400

Q6. घन की भुजा 10 सेमी है। दिया गया है, E अर्धवृत्त का केंद्र है और यह दिए गए घन के विकर्ण का मध्य-बिंदु है।

मात्रा I: छायांकित भाग का क्षेत्रफल।
मात्रा II: 10 वर्ग सेमी
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं है

Q7. 45 किमी/घंटा की गति से चलने वाली एक पैसेंजर ट्रेन की लंबाई 250 मीटर है। राजधानी ट्रेन की लंबाई 750 मीटर है जो अधिकतम 135 किमी/घंटा की गति से चल सकती है।
मात्रा I: पैसेंजर ट्रेन द्वारा प्लेटफार्म पर खड़े व्यक्ति को पार करने में लगा समय।
मात्रा II: विपरीत दिशा से आ रही राजधानी ट्रेन को पार करने में पैसेंजर ट्रेन द्वारा लिया गया समय।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं है

Q8. 3 बर्तन A, B और C दूध और पानी के मिश्रण से भरे हुए हैं। बर्तन A में 5 लीटर पानी और 25 लीटर दूध है, बर्तन B में 15 लीटर पानी और 30 लीटर दूध है और बर्तन C में पानी और दूध का अनुपात 1 : 5 है। बर्तन A, B और C से क्रमशः कुल मिश्रण का 20%, 40% और 30% लिया जाता है और एक चौथे बर्तन में डाला जाता है। चौथे बर्तन में दूध और पानी का अनुपात 16 : 5 है।
मात्रा I: बर्तन C की क्षमता (लीटर में)
मात्रा II: 80 लीटर
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं है

Q9. P, Q और R एक कार्य को क्रमशः 8, 12 और 24 दिनों में पूरा कर सकते हैं। वे वैकल्पिक दिनों में काम करते हैं।
मात्रा I: उनके द्वारा कार्य को पूरा करने में लिया गया समय यदि P पहले दिन कार्य करता है, Q दूसरे दिन कार्य करता है और R तीसरे दिन कार्य करता है और इसी प्रकार आगे भी।
मात्रा II: उनके द्वारा कार्य को पूरा करने में लिया गया समय यदि Q पहले दिन कार्य करता है, R दूसरे दिन कार्य करता है और P तीसरे दिन कार्य करता है और इसी प्रकार आगे भी।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं है

Q10. दो थैले A और B हैं। थैले A में 5 लाल, 3 हरी और 4 नीली गेंदें हैं जबकि थैले B में 8 नीली, 4 हरी और 6 लाल गेंदें हैं।
मात्रा I: यदि बैग B से यादृच्छिक रूप से 3 गेंदें निकाली जाती हैं, तो अधिक से अधिक 1 लाल गेंद प्राप्त करने की प्रायिकता।
मात्रा II: बैग A से यादृच्छिक रूप से 3 गेंदों को निकालने पर कम से कम 2 लाल गेंदों को प्राप्त करने की प्रायिकता।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं है

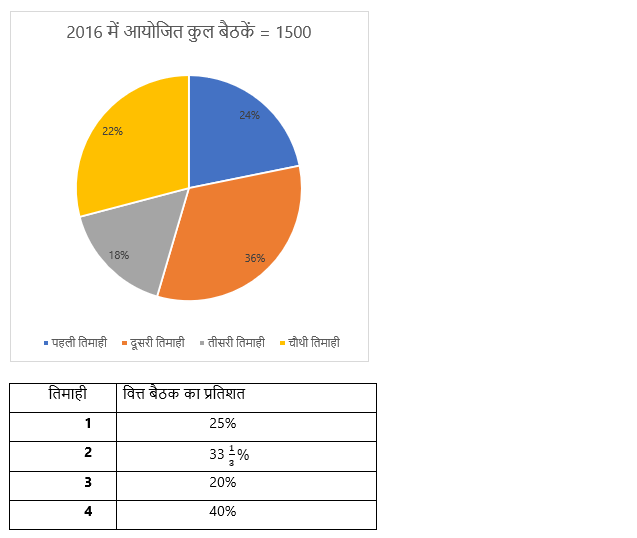
Directions (11 -15): नीचे दिया गया पाई चार्ट 2016 की चार तिमाहियों में आयोजित कुल बैठकों का प्रतिशत वितरण दर्शाता है, जबकि तालिका इन चार तिमाहियों में आयोजित वित्त बैठकों का प्रतिशत दर्शाती है। आंकड़ों को ध्यानपूर्वक पढ़ें और प्रश्नों के उत्तर दें।
नोट – प्रत्येक तिमाही में तीन (वित्त, प्रबंधन और व्यय) प्रकार की बैठकें आयोजित की जाती हैं।

Q11. यदि तीसरी तिमाही में आयोजित कुल प्रबंधन बैठकें उस तिमाही में आयोजित कुल व्यय बैठकों से 40% अधिक हैं और चौथी तिमाही में आयोजित कुल प्रबंधन बैठकें उस तिमाही में आयोजित कुल व्यय बैठकों से 20% अधिक हैं, तो तीसरी और चौथी तिमाही में आयोजित कुल प्रबंधन बैठकों के बीच अंतर ज्ञात कीजिए।
(a) 14
(b) 18
(c) 16
(d) 12
(e) 20

Q13. यदि दूसरी तिमाही में आयोजित कुल व्यय बैठक उस तिमाही में आयोजित कुल प्रबंधन बैठक से 40% कम है, तो दूसरी तिमाही में आयोजित कुल व्यय बैठक, पहली तिमाही में आयोजित कुल प्रबंधन और व्यय बैठक से कितने प्रतिशत कम है?
(a) 40%
(b) 45%
(c) 25%
(d) 60%
(e) 50%

Q14. यदि 2017 की पहली तिमाही में आयोजित कुल बैठकें 2016 की पहली और तीसरी तिमाही में आयोजित कुल वित्त बैठक से 25% अधिक हैं और 2017 की पहली तिमाही में आयोजित वित्त बैठक, प्रबंधन बैठक और व्यय बैठक का अनुपात 9 : 7 : 5 है, तो 2017 की पहली तिमाही में आयोजित कुल प्रबंधन बैठक का 2016 की दूसरी तिमाही में आयोजित कुल वित्त बैठक से अनुपात ज्ञात कीजिये।
(a) 1: 4
(b) 1 : 2
(c) 1 : 5
(d) 1 : 3
(e) इनमें से कोई नहीं

Q15. पहली, दूसरी और चौथी तिमाही में आयोजित कुल प्रबंधन बैठकें क्रमशः इन तिमाही में आयोजित कुल व्यय बैठकों की तुलना में 25%, 40% और 20% अधिक हैं। यदि तीसरी तिमाही में आयोजित कुल प्रबंधन और व्यय बैठकें बराबर हैं, तो 2016 की इन चार तिमाहियों में आयोजित प्रबंधन बैठकों की औसत संख्या ज्ञात कीजिए।
(a) 142
(b) 152
(c) 144
(d) 148
(e) 140

Solutions: