Q1.
एक बैंक 5000 रुपये से कम मूल राशि पर 10% का साधारण ब्याज प्रदान करता है अन्यथा 20% प्रदान करता है। एक आदमी ने 3 साल के लिए A रुपये का निवेश किया। A का मान क्या है?
(A) यदि उसने 3000 रुपये अधिक जमा किए होते, तो उसे 900 रुपये का ब्याज अधिक मिलता।
(B) यदि उसने 4000 रुपये अधिक जमा किए होते, तो उसे 2400 रुपये का ब्याज अधिक मिलता।
(C) A का मान 500 का गुणक है।
(a) या तो A और B या B और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(b) या तो A और B या A और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(c) या तो A और C या B और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(d) A, B और C एक साथ प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(e) सभी कथन मिलकर भी प्रश्न का उत्तर देने के लिए पर्याप्त नहीं हैं।
Q2. एक आदमी के पास दो वस्तुएँ A और B हैं। वस्तु B का विक्रय मूल्य क्या है?
(A) वस्तु A के 4 और वस्तु B के 1 को बेचने के बाद प्राप्त राशि 70 रुपये है। इस राशि से वह या तो वस्तु A के 7 को खरीद सकता है या वस्तु B के 4 के साथ वस्तु A के 1 को खरीद सकता है।
(B) वस्तु B के 1 को बेचने पर अर्जित लाभ 3 रुपये है और वस्तु A के 1 को बेचने पर अर्जित लाभ% 30% है। वस्तु B का विक्रय मूल्य और क्रय मूल्य क्रमशः वस्तु A की तुलना में 5 रुपये अधिक हैं।
(C) A और B पर अर्जित लाभ% का अनुपात 3:2 है और उनके क्रय मूल्य का अनुपात क्रमशः 2:3 है। सभी लाभ %, क्रय मूल्य और विक्रय मूल्य का मान पूर्णांक है।
(a) या तो A और B या B और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(b) या तो A और B या A और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(c) या तो A और C या B और C प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(d) A, B और C एक साथ प्रश्न का उत्तर देने के लिए पर्याप्त हैं
(e) या तो केवल B या A और C मिलकर प्रश्न का उत्तर देने के लिए पर्याप्त हैं
Directions (3-5): दिए गए प्रश्नों में दो मात्राएँ,’मात्रा I’ और ‘मात्रा II’, दी गई हैं। आपको दोनों मात्राओं के बीच संबंध निर्धारित करना है और उचित विकल्प चुनना है:
Q3. एक आदमी ने दो योजनाओं ‘A’ और B में 8:11 के अनुपात में निवेश किया। योजना ‘A’ ने चक्रवृद्धि ब्याज दिया, जबकि योजना ‘B’ ने साधारण ब्याज दिया।
मात्रा I – योजना ‘B’ में निवेश की गई राशि।
यदि योजना ‘A’ और ‘B’ में दी जाने वाली ब्याज की दर क्रमशः 20% वार्षिक और 16% वार्षिक थी और व्यक्ति को दो वर्षों के बाद दोनों योजनाओं से कुल ब्याज के रूप में 3520 रुपये प्राप्त हुए।
मात्रा II – योजना ‘A’ में आदमी द्वारा निवेश की गई राशि।
यदि योजना ‘A’ और ‘B’ में दी जाने वाली ब्याज दर क्रमशः 10% प्रति वर्ष और 20% प्रति वर्ष थी और आदमी को दो वर्ष बाद योजना ‘B’ से ब्याज के रूप में A की तुलना में 1870 रुपये अधिक मिलते हैं।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q4. एक थैले में 9 पीली गेंदें, Y हरी गेंदें और 7 लाल गेंदें हैं, यदि थैले में से एक गेंद यादृच्छया निकाली जाती है तो इसके हरे होने की प्रायिकता 5/21 है।
मात्रा I – कम से कम एक फल के सेब होने की प्रायिकता, जब बाल्टी P से दो फल बिना प्रतिस्थापन के निकाले जाते हैं।
बाल्टी ‘P’ में 2Y सेब, 3(Y – 2) केला और 1.5(Y – 1) संतरे हैं।
मात्रा II – बाल्टी Q में से दो पासे बिना प्रतिस्थापन के निकाले जाने पर दोनों पासों के एक ही रंग के होने की प्रायिकता है।
थैले ‘Q’ में 4 लाल पासे, 3.5 (Y – 3) हरे पासे और 2Y पीले पासे हैं।
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Q5. दो बर्तन A और B में दूध और पानी का मिश्रण क्रमशः (X + 54) लीटर और (X + 84) लीटर है। बर्तन A और बर्तन B में दूध और पानी का अनुपात क्रमश: 3 : 2 और 2 : 1 है।
मात्रा I – बर्तन B में दूध की मात्रा।
यदि बर्तन A से 60% मिश्रण और बर्तन B से 662/3% मिश्रण निकाला जाता है, तो दोनों बर्तनों में शेष मिश्रण बराबर है।
मात्रा II – 144 लीटर
(a) मात्रा I > मात्रा II
(b) मात्रा I < मात्रा II
(c) मात्रा I ≥ मात्रा II
(d) मात्रा I ≤ मात्रा II
(e) मात्रा I = मात्रा II या कोई संबंध नहीं
Direction (6-10): – एक स्कूल में चार छात्रावास हैं जिनमें दो वर्ग हैं एक लड़कों के लिए और एक लड़कियों के लिए। नीचे दिया गया लाइन चार्ट 2012 (पिछले वर्ष) की तुलना में 2013 में इन छात्रावासों में कुल छात्रों की संख्या में वृद्धि/कमी दर्शाता है। नीचे दी गई तालिका 2013 में इन छात्रावासों में लड़कों की संख्या का लड़कियों की संख्या से अनुपात दर्शाती है। आँकड़ों का ध्यानपूर्वक अध्ययन कीजिए और निम्नलिखित प्रश्नों के उत्तर दीजिए।
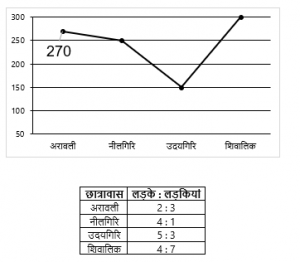
Q6. अरावली में, 2013 में लड़कियों की संख्या 2012 की तुलना में 20% अधिक है। यदि अरावली में लड़कियों की संख्या में परिवर्तन अरावली में लड़कों की संख्या में परिवर्तन से 25% अधिक है, तो 2013 में अरावली में लड़कों की संख्या ज्ञात कीजिए।
(a) 900
(b) 600
(c) 500
(d) 750
(e) 800
Q7. 2012 की तुलना में 2013 में क्रमशः अरावली और नीलगिरि में छात्रों की संख्या में वृद्धि और कमी हुई है। अरावली छोड़ने वाली लड़कियों की संख्या नीलगिरि में शामिल हो जाती है (लड़कियों की संख्या में कोई अन्य परिवर्तन नहीं है) जैसे कि 2012 की तुलना में 2013 में अरावली और नीलगिरि में लड़कों की संख्या में वृद्धि और कमी के बीच अनुपात 16 : 15 है। तो नीलगिरि में लड़कों की संख्या में परिवर्तन ज्ञात कीजिए।
(a) 350
(b) 320
(c) 300
(d) 420
(e) 400
Q8. 2012 में, उदयगिरि और शिवालिक में लड़कों की संख्या बराबर है और शिवालिक में लड़कियों की संख्या उदयगिरि में लड़कियों की संख्या से 540 अधिक है। यदि 2013 में, दोनों छात्रावासों में लड़कों की संख्या बराबर है, तो शिवालिक में कुल छात्रों की संख्या ज्ञात कीजिए, यदि 2013 में दोनों छात्रावासों की संख्या पिछले वर्ष की तुलना में बढ़ जाती है।
(a) 1650
(b) 1200
(c) 960
(d) 1500
(e) 900
Q9. 2012 और 2013 में उदयगिरि की कुल संख्या का नीलगिरि की कुल संख्या से अनुपात क्रमशः 4 : 5 और 5 : 8 है। यदि उदयगिरि की कुल संख्या घट जाती है, तो 2012 में नीलगिरि की कुल संख्या ज्ञात कीजिए।
(a) 1600
(b) 1200
(c) 1250
(d) 1400
(e) 1750
Q10. 2013 में, सभी छात्रावासों की संख्या 2012 की तुलना में बढ़ जाती है। यदि 2012 में छात्रावासों की कुल संख्या 1030 है, तो ज्ञात कीजिए कि 2013 में अरावली में लड़कों की संख्या 2013 में उदयगिरि में लड़कों की संख्या से कितनी अधिक है, यह दिया गया है कि अरावली, नीलगिरि, उदयगिरि और शिवालिक की संख्या का अनुपात क्रमशः 2 : 3 : 2 : 3 है।
(a) 80
(b) 100
(c) 120
(d) 90
(e) 10
Solutions:










 रिशभ भारती की प्रेरणादायक कहानी: असफलताओ...
रिशभ भारती की प्रेरणादायक कहानी: असफलताओ...
 RRB NTPC Graduate Exam Schedule 2026 Out...
RRB NTPC Graduate Exam Schedule 2026 Out...
 Banking Exam Calendar 2026: जानिए कब आएग...
Banking Exam Calendar 2026: जानिए कब आएग...










