संख्यात्मक क्षमता अनुभाग ने उम्मीदवारों के रोंगटे खड़े कर देता है, जब वे बैंकिंग परीक्षा के लिए उपस्थित होते हैं। चूंकि हर दूसरे खंड का स्तर केवल जटिल और शांत होता जा रहा है, इसमें कोई संदेह नहीं है कि यह खंड भी आपके जोश को ठंडा कर देता है। इस खंड में पूछे गए प्रश्न गणनात्मक और बहुत समय लेने वाले हैं। लेकिन एक बार उचित रणनीति, गति और सटीकता से निपटने के बाद, यह अनुभाग आपको परीक्षा में अधिकतम अंक प्राप्त करवा सकता है। सर्वोत्तम पैटर्न के साथ अभ्यास करने में आपकी सहायता के लिए संख्यात्मक क्षमता प्रश्नोत्तरी निम्नलिखित है।
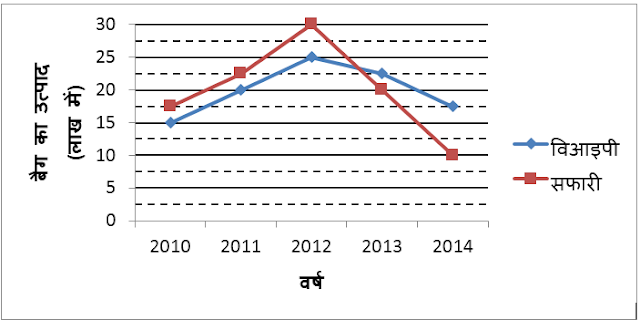
Directions (1-5): निम्नलिखित रेखा आरेख पांच अलग-लग वर्षों में दो कंपनी वीआईपी और सफारी दो कंपनियों के बैग के उत्पाद (लाखों में) को दर्शाता है।
ग्राफ का अध्ययन कीजिये और निम्नलिखित प्रश्नों के उत्तर दीजिये
Q1. दिए गये सभी वर्षों में विआइपी की औसत संख्या ज्ञात कीजिये।
25 लाख
20 लाख
15 लाख
27 लाख
इनमें से कोइ नहीं
Solution:
Required average =1/5×(15+20+25+22.5+17.5) =20 lakhs
Q2. सफारी बैगों की तुलना में वीआईपी बैग का उत्पादन किस वर्ष में कम है?
2012
2013
2014
2010
2011
Solution:
From graph it is clear that the require year is 2012
Q3. वर्ष 2014 में विआइपी बैग का उत्पादन सफारी बैग के उत्पादन से कितने प्रतिशत अधिक है?
65%
80%
75%
70%
इनमें से कोई नहीं
Solution:
Required percentage=(17.5-10)/10×100 =75%
Q4. वर्ष 2010, 2011 और 2013 में मिलाकर सफारी बैग के कुल उत्पादन का उसी वर्ष में विआइपी बैग के कुल उत्पादन से अनुपात कितना है?
23 : 22
25 : 24
23 : 24
24 : 23
इनमें से कोई नहीं
Solution:
Required ratio = (17.5 + 22.5 + 20) : (15 + 20 + 22.5)
= 60 : 57.5
= 24 : 23
Q5. सभी वर्षों में दोनों कंपनियों में बैग के कुल उत्पादन के बीच अंतर (लाखों में) कितना है?
0
2
4
6
1
Solution:
Required difference = (17.5 + 22.5 + 30 + 20 + 10) – (15 + 20 + 25 + 22.5 + 17.5) = 0
Directions (6-10):निम्नलिखित प्रत्येक प्रश्न में दो समीकरण दिए गए हैं। समीकरणों को हल कीजिये और
उत्तर दोजिये–
उत्तर दोजिये–
Q6. I. 3x² + 16x + 21 = 0
II. 6y² + 17y + 12 = 0
यदि x < y
यदि x ≤ y
x और y के बीच कोई संबंध निर्धारित नहीं किया जा सकता
यदि x ≥ y
यदि x > y
Solution:
I. 3x² + 16x + 21 = 0
⇒ 3x² + 9x + 7x + 21 = 0
⇒ (x + 3) (3x + 7) = 0
⇒ x = –3, –7/3
II. 6y² + 17y + 12 = 0
⇒ 6y² + 9y + 8y + 12 = 0
⇒ 3y (2y + 3) + 4 (2y + 3) = 0
⇒ y = – 3/2, –4/3
y > x
Q7. I. 16x² + 20x + 6 = 0
II. 10y² + 38y + 24 = 0
यदि x < y
यदि x ≤ y
x और y के बीच कोई संबंध निर्धारित नहीं किया जा सकता
यदि x ≥ y
यदि x > y
Solution:
I. 16x² + 20x + 6 = 0
⇒ 8x² + 10x + 3 = 0
⇒ 8x² + 4x + 6x + 3 = 0
⇒ (2x + 1) (4x + 3) = 0
⇒ x = –1/2, –3/4
II. 10y² + 38y + 24 = 0
⇒ 5y² + 19y + 12 = 0
⇒ 5y² + 15y + 4y + 12 = 0
⇒ (y + 3) (5y + 4) = 0 y
= –3, –4/5
x > y
Q8. I. 8x² + 6x = 5
II. 12y² – 22y + 8 = 0
यदि x < y
यदि x ≤ y
x और y के बीच कोई संबंध निर्धारित नहीं किया जा सकता
यदि x ≥ y
यदि x > y
Solution:
I. 8x² + 6x – 5 = 0
⇒ 8x² + 10x – 4x – 5 = 0
⇒ (4x + 5) (2x – 1) = 0
⇒ x = ½, –5/4
II. 12y² – 22y + 8 = 0
⇒ 6y² – 11y + 4 = 0
⇒ 6y² – 3y – 8y + 4 = 0
⇒ (2y – 1) (3y – 4) = 0
⇒ y = 1/2, 4/3
y ≥ x
Q9. I. 17x² + 48x = 9
II. 13y² = 32y – 12
यदि x < y
यदि x ≤ y
x और y के बीच कोई संबंध निर्धारित नहीं किया जा सकता
यदि x ≥ y
यदि x > y
Solution:
I. 17x² + 48x – 9 = 0
⇒ 17x² + 51x – 3x – 9 = 0
⇒ (x + 3) (17x – 3) = 0
⇒ x = 3/17, – 3
II. 13y² – 32y + 12 = 0
⇒ 13y² – 26y – 6y + 12 = 0
⇒ (y – 2) (13y – 6) = 0
⇒ y = 2, 6/13
y > x
Q10. I. 8x² + 26x + 15 = 0
II. 4y² + 24y + 35 = 0
यदि x < y
यदि x ≤ y
x और y के बीच कोई संबंध निर्धारित नहीं किया जा सकता
यदि x ≥ y
यदि x > y
Solution:
I. 8x² + 26x + 15 = 0
⇒ 8x² + 20x + 6x + 15 = 0
⇒ 4x (2x + 5) + 3(2x + 5) = 0
⇒ (2x + 5) (4x + 3) = 0
⇒ x = – 5/2, –3/4
II. 4y² + 24y + 35 = 0
⇒ 4y² + 10y + 14y + 35 = 0
⇒ 2y (2y + 5) + 7 (2y + 5) = 0
⇒ (2y + 5) (2y + 7) = 0
⇒ y = –5/2, –7/2
x ≥ y
Q11. सोहन एक राशि का 23% बीमा पॉलिसी पर, 33% भोजन पर, 19% बच्चों की शिक्षा पर और 16% मनोरंजन पर खर्च करता है। वह बैंक में 504 रुपये की शेष राशि जमा करता है। वह भोजन और बीमा पॉलिसी में मिलाकर कुल कितनी राशि खर्च करता है?
3200 रु.
3126 रु.
3136 रु.
3080 रु.
3800 रु.
Solution:
Remaining sum (in percentage)
=100 – (23+33+19+16)
= 9%
∵ 9% → 504
∴100%→504/9×100
→5600
∴ Required answer= ((33+23))/100×5600
=Rs. 3136
Q12. एक त्रिभुजाकार मैदान का आधार इसकी ऊंचाई का तिगुना है। यदि 50 रुपये प्रति हेक्टेयर की दर से खेती करने की लागत 675 रुपये है, तो इसका आधार और ऊँचाई ज्ञात कीजिए। (1 हेक्टेयर = 10000 वर्ग मीटर)
900 मी, 300 मी
350 मी, 850 मी
750 मी, 450 मी
875 मी, 325 मी
इनमें से कोई नहीं
Solution:
Area of the field
= (Total cost)/Rate=675/50
= 13.5 hectares
= (13.5 × (10000) m²
= 135000 m²
Let altitudes = x m
∴ base = 3x m
Now, ½ × 3x × x=135000
⇒ x² = 90000
⇒ x = 300 metres
& base 900 metres
Q13. एक महिला द्वारा 8 घंटे में किया गया कार्य, एक पुरुष द्वारा 6 घंटे में किए गए कार्य और एक लड़के द्वारा 12 घंटे में किये गये के कार्य के बराबर है। यदि प्रति दिन 6 घंटे कार्य करके 9 पुरुष 6 दिनों में एक कार्य को पूरा कर सकते हैं, तो प्रति दिन 8 घंटे कार्य करके 12 पुरुष, 12 महिलाएं और 12 लड़के मिलकर कितने दिन में कार्य पूरा कर सकते हैं?
2½ दिन
1½ दिन
3½ दिन
4½ दिन
इनमें से कोई नहीं
Solution:
Ratio of efficiencies of man, women and child
=1/6 :1/8 :1/12
= 4 : 3 : 2
∴ One day one hour work of all of them will be respectively
=1/(36×9), 3/(4×36×9) & 1/(2×36×9)
∴ One day work of (12M + 12W + 12B)
=(12×8)/(36×9)+(12×8×3)/(4×36×9)+(12×8)/(2×36×9)
=2/3
∴ Required days to complete the work
=3/2 days
=1½ days
Q14. दो ट्रेनें स्टेशन A और B से आरम्भ होती हैं और क्रमशः 50 किमी/घंटे और 60 किमी/घंटे की गति से एक-दूसरे की ओर यात्रा करती हैं। उनकी मिलने के समय पर दूसरी ट्रेन पहली से 100 किमी अधिक यात्रा कर चुकी है। A और B के बीच की दूरी है:
990 किमी
1200 किमी
1100 किमी
1440 किमी
1240 किमी
Solution:
Let first train travelled x km before meeting
∴ Second train will travel (x +100) km before meeting in same time as that by first.
(x+100)/60=x/50
⇒ x = 500 km
∴ Required distance = 2 × 500 + 100
= 1100 km
Q15. एक घनाभ के तीन क्रमागत फलक का क्षेत्रफल 12 वर्ग सेमी,20 वर्ग सेमी और 15 वर्ग सेमी हैं, तो घनाभ का आयतन (घन सेमी में) है-
3600
100
80
60
120
Solution:
Let length, breadth and height of the cuboid be x, y and z.
Then, area of three consecutive faces, i.e.,
xy, yz and zx is 12, 20 and 15, respectively
∴ x² y² z²=12×20×15
xyz = √(12×20×15)=60 cm³
FCI Phase I क्वांट क्विज 2023 - 6th Janu...
SBI Clerk Prelims क्वांट क्विज 2022 : 13...
Quantitative Aptitude Quiz For IBPS PO M...
