प्रिय उम्मीदवारों,
संख्यात्मक क्षमता अनुभाग ने उम्मीदवारों के रोंगटे खड़े कर देता है, जब वे बैंकिंग परीक्षा के लिए उपस्थित होते हैं। चूंकि हर दूसरे खंड का स्तर केवल जटिल और शांत होता जारहा है, इसमें कोई संदेह नहीं है कि यह खंड भी आपके जोश को ठंडा कर देता है। इस खंड में पूछे गए प्रश्न गणनात्मक और बहुत समय लेने वाले हैं। लेकिन एक बार उचित रणनीति, गति और सटीकता से निपटने के बाद, यह अनुभाग आपको परीक्षा में अधिकतम अंक प्राप्त करवा सकता है। सर्वोत्तम पैटर्न के साथ अभ्यास करने में आपकी सहायता के लिए संख्यात्मक क्षमता प्रश्नोत्तरी निम्नलिखित है।
Directions (1-5):निम्नलिखित प्रश्नों में, I और II दो समीकरण दिए गए हैं। दोनों समीकरणों को हल कीजिए और उत्तर दीजिए-
Q1. (i) x² – 16x + 63 = 0
(ii) y² – 22y + 117 = 0
यदि x > y
यदि x < y
यदि x ≤ y
यदि x ≥ y
यदि x = y या x और y के मध्य संबंध स्थापित नहीं किया जा सकता
Solution:
(i) x² – 16x + 63 = 0
x² – 7x – 9x + 63 = 0
(x – 7) (x – 9) = 0
x = 7, 9
(ii) y² – 22y + 117 = 0
y² – 9y – 13y + 117 = 0
(y – 9) (y – 13) = 0
y = 9, 13
y ≥ x
x² – 7x – 9x + 63 = 0
(x – 7) (x – 9) = 0
x = 7, 9
(ii) y² – 22y + 117 = 0
y² – 9y – 13y + 117 = 0
(y – 9) (y – 13) = 0
y = 9, 13
y ≥ x
Q2. (i) x² – 3x – 18 = 0
(ii) 2y² + 11y + 14 = 0
यदि x > y
यदि x < y
यदि x ≤ y
यदि x ≥ y
यदि x = y या x और y के मध्य संबंध स्थापित नहीं किया जा सकता
Solution:
(i) x² – 3x – 18 = 0
x² - 6x + 3x – 18 = 0
x (x – 6) + 3 (x – 6) = 0
(x – 6) (x + 3)
x = –3, 6
(ii) 2y² + 11y + 14 = 0
2y² + 7y + 4y + 14 = 0
y (2y + 7) + 2 (2y + 7) = 0
(y + 2) (2y + 7) = 0
y=–7/2, –2 No relation between x & y
x² - 6x + 3x – 18 = 0
x (x – 6) + 3 (x – 6) = 0
(x – 6) (x + 3)
x = –3, 6
(ii) 2y² + 11y + 14 = 0
2y² + 7y + 4y + 14 = 0
y (2y + 7) + 2 (2y + 7) = 0
(y + 2) (2y + 7) = 0
y=–7/2, –2 No relation between x & y
Q3. (i) x² – 23x + 120 = 0
(ii) y² – y – 42 = 0
यदि x > y
यदि x < y
यदि x ≤ y
यदि x ≥ y
यदि x = y या x और y के मध्य संबंध स्थापित नहीं किया जा सकता
Solution:
(i) x² – 23x + 120 = 0
x² – 15x – 8x + 120 = 0
x (x – 15) – 8 (x – 15) = 0
(x – 8) (x – 15) = 0
x = 8, 15
(ii) y² – y – 42 = 0
y² – 7y + 6y – 42 = 0
y (y – 7) + 6 (y – 7) = 0
(y + 6) (y – 7) = 0
y = –6, 7
x > y
x² – 15x – 8x + 120 = 0
x (x – 15) – 8 (x – 15) = 0
(x – 8) (x – 15) = 0
x = 8, 15
(ii) y² – y – 42 = 0
y² – 7y + 6y – 42 = 0
y (y – 7) + 6 (y – 7) = 0
(y + 6) (y – 7) = 0
y = –6, 7
x > y
Q4. (i) 2x² – 13x + 15 = 0
(ii) 2y² + 11 y – 21 = 0
यदि x > y
यदि x < y
यदि x ≤ y
यदि x ≥ y
यदि x = y या x और y के मध्य संबंध स्थापित नहीं किया जा सकता
Solution:
(i) 2x² – 13x + 15 = 0
2x² – 10x – 3x + 15 = 0
2x (x – 5) – 3 (x – 5) = 0
(2x – 3) (x – 5) = 0
x = 3/2, 5
(ii) 2y² + 11 y – 21 = 0
2y² + 14y – 3y – 21 = 0
2y (y + 7) – 3 (y + 7) = 0
(2y – 3) (y + 7) = 0
y=–7, 3/2
x ≥ y
2x² – 10x – 3x + 15 = 0
2x (x – 5) – 3 (x – 5) = 0
(2x – 3) (x – 5) = 0
x = 3/2, 5
(ii) 2y² + 11 y – 21 = 0
2y² + 14y – 3y – 21 = 0
2y (y + 7) – 3 (y + 7) = 0
(2y – 3) (y + 7) = 0
y=–7, 3/2
x ≥ y
Q5. (i) x² = 36
(ii) y³ = 216
यदि x > y
यदि x < y
यदि x ≤ y
यदि x ≥ y
यदि x = y या x और y के मध्य संबंध स्थापित नहीं किया जा सकता
Solution:
(i) x² = 36
x = –6, +6
(ii) y³ = 216
y = 6
x ≤ y
x = –6, +6
(ii) y³ = 216
y = 6
x ≤ y
Directions (6-10): निम्नलिखित दिए गए प्रश्नों में प्रश्न चिह्न (?) के स्थान में क्या आना चाहिए (नोट: सटीक मान की गणना आवश्यक नहीं।) ?
Q6. 2.99/6.98÷291.01/238.02×387.98+46.02% 444.98= ?
320
361
381
241
341
Solution:
?=3/7×238/291×388+46/100×445
=136 + 204.7
= 341
=136 + 204.7
= 341
Q7. (2.87)²+(11.87)²+(9.08)²+(6.89)²=?
283
251
315
213
173
Solution:
9+144+81+49=283
Q8. √288.98×16.99+1083.11÷56.89=?
364
308
393
345
413
Solution:
=17×17+19
=289+19
=308
=289+19
=308
Q9. 94.89×12.93+√36.08×14.94=53.06×√(?)
144
625
441
729
961
Solution:
1235+6×15=53×√x
√x=25
x=625
√x=25
x=625
Q10. (639.93 का 239.98 %)÷(7.94)2 =?
36
36
45
39
24
69
Solution:
240/100×640×1/64=24
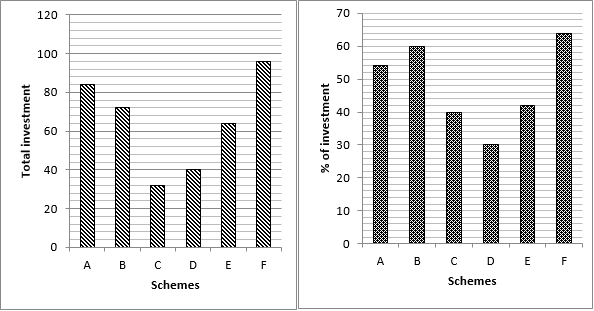
Directions (11-15): नीचे दिए गए बार ग्राफ का ध्यानपूर्वक अध्ययन करके निम्नलिखित प्रश्नों के उत्तर दीजिए.
नीचे दिया गया बार ग्राफ में 6 योजनाओं (A, B, C, D, E और F) में रिचा और दीक्षा की कुल निवेश और उसमें से रिचा का निवेश प्रतिशत (हजारों में) दर्शाया गया है.
नीचे दिया गया बार ग्राफ में 6 योजनाओं (A, B, C, D, E और F) में रिचा और दीक्षा की कुल निवेश और उसमें से रिचा का निवेश प्रतिशत (हजारों में) दर्शाया गया है.
Q11. योजना A एक निश्चित ब्याज दर (प्रतिशत प्रतिवर्ष) पर साधारण ब्याज प्रदान करती है. यदि योजना A से 4 वर्ष बाद रिचा और दीक्षा द्वारा प्राप्त कुल ब्याज के मध्य का अंतर 4435.20 रूपये है, तो ब्याज दर (प्रतिशत प्रतिवर्ष) कितनी है?
17.5
18
16.5
20
15
Solution:
Amount invested by Richa in scheme A = 54% of 84000 = Rs. 45360
∴ Amount invested by Diksha in scheme A = 84000 – 45360 = Rs. 38640
Let the required rate be r% per annum. Then,
= (45360×r×4)/100-(38640×r×4)/100 = 4435.20
⇒6720×r×4 = 443520
⇒ r = 16.5%
∴ Amount invested by Diksha in scheme A = 84000 – 45360 = Rs. 38640
Let the required rate be r% per annum. Then,
= (45360×r×4)/100-(38640×r×4)/100 = 4435.20
⇒6720×r×4 = 443520
⇒ r = 16.5%
Q12. रिचा द्वारा योजना C और E में एकसाथ निवेश राशि और उसी योजना में दीक्षा द्वारा निवेश की गई कुल राशि के मध्य का क्रमश: अनुपात कितना है?
31 : 44
31 : 42
27 : 44
35 : 48
29 : 38
Solution:
Required ratio = (Total amount invested by Richa in schemes C and E together): (Total amount invested by Diksha in schemes C and E together)
= (40% of 32000 + 42% of 64000): (60% of 32000 + 58% of 64000)
= 39680: 56320 = 31: 44
= (40% of 32000 + 42% of 64000): (60% of 32000 + 58% of 64000)
= 39680: 56320 = 31: 44
Q13. यदि योजना C 12% प्रतिवर्ष पर चक्रवृधि ब्याज (वार्षिक संयोजित) प्रदान करती है, तो 2 वर्ष बाद योजना C से रिचा और दीक्षा द्वारा प्राप्त ब्याज के मध्य का अंतर कितना है?
1628.16 रु.
1584.38 रु.
1672.74 रु.
1536.58 रु.
1722.96 रु.
Solution:
Difference of amount invested by Richa and Diksha in
Scheme C = 60% of 32000 – 40% of 32000 = 20% of 32000 = Rs. 6400
∴ Required difference in their interest
=6400[(1+12/100)²-1]=6400×0.2544=Rs.1628.16
Scheme C = 60% of 32000 – 40% of 32000 = 20% of 32000 = Rs. 6400
∴ Required difference in their interest
=6400[(1+12/100)²-1]=6400×0.2544=Rs.1628.16
Q14. दीक्षा ने योजना F में 4 वर्ष के लिए निवेश किया. यदि योजना F पहले दो वर्षों के लिए 7% प्रतिवर्ष पर साधारण ब्याज प्रदान करती है और तीसरे और चौथे वर्ष के लिए 10% प्रतिवर्ष पर चक्रवृधि ब्याज (वार्षिक संयोजित) प्रदान करती है, तो 4 वर्ष बाद दीक्षा द्वारा प्राप्त ब्याज कितना होगा?
13548.64 रु.
13112.064 रु.
12242.5 रु.
12364 रु.
11886 रु.
Solution:
Amount invested by Diksha in investment F
= (100 – 64) % of 96000 = 36% of 96000 = Rs. 34560
Then, total interest earned by Diksha after 4 years
= (34560×7×2)/100+(34560+SI of first 2 years)[(1+10/100)²-1] = 4838.40 + 8273.664 = Rs. 13112.064
= (100 – 64) % of 96000 = 36% of 96000 = Rs. 34560
Then, total interest earned by Diksha after 4 years
= (34560×7×2)/100+(34560+SI of first 2 years)[(1+10/100)²-1] = 4838.40 + 8273.664 = Rs. 13112.064
Q15. रिचा द्वारा योजना G में निवेश की गई राशी उसके द्वारा योजना B में निवेश की गई राशि के समान है. योजना G और B की ब्याज दर समान है. केवल अंतर इतना है कि योजना G चक्रवृद्धि ब्याज (वार्षिक संयोजित) प्रदान करता है, जबकि योजना B साधारण ब्याज प्रदान करता है. यदि 2 वर्ष बाद रिचा द्वारा दोनों योजना से प्राप्त ब्याज के मध्य का अंतर 349.92 है, तो ब्याज दर कितनी है?
9%
5%
13%
11%
7%
Solution:
Amount invested by Richa in each of scheme G and B
= 60% of 72000 = 43200
Let the rate of interest be r% per annum.
Then, according to the question,
C.I -S.I. = PR²/100² (for two years)
349.92= 43200×r²/100²
or, r²=81
∴ r = 9%
= 60% of 72000 = 43200
Let the rate of interest be r% per annum.
Then, according to the question,
C.I -S.I. = PR²/100² (for two years)
349.92= 43200×r²/100²
or, r²=81
∴ r = 9%





 IBPS PO Prelims क्वांट क्विज 2022 : 13th...
IBPS PO Prelims क्वांट क्विज 2022 : 13th...










