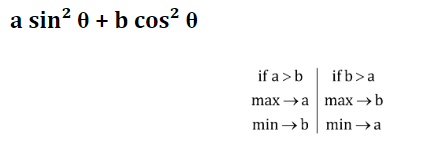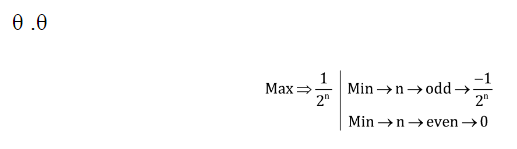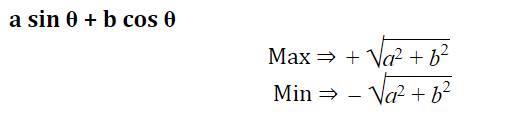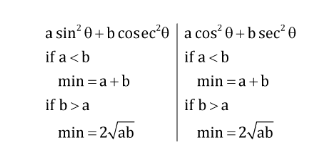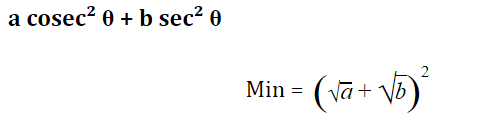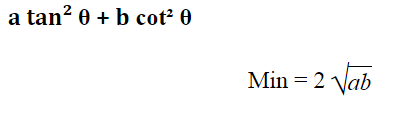त्रिकोणमिति (Trigonometry) गणित की वह प्रमुख शाखा है जिसमें त्रिभुजों, विशेष रूप से समकोण त्रिभुज और उनसे बनने वाले विभिन्न बहुभुजों का अध्ययन किया जाता है। शब्द “त्रिकोणमिति” ग्रीक शब्दों trigōnon (अर्थात् “triangle”) और metron (अर्थात् “measure”) से बना है, जिसका शाब्दिक अर्थ है “त्रिभुज का मापन”। यह विषय त्रिभुज की भुजाओं और कोणों के बीच संबंधों को समझने में मदद करता है, और इसका उपयोग भौतिकी, इंजीनियरिंग, नौवहन, तथा खगोलशास्त्र जैसे अनेक क्षेत्रों में किया जाता है।
Trigonometry | Definition, Formulas, Ratios, & Identities in Hindi
Trigonometry यानी त्रिकोणमिति, क्वांटिटेटिव एप्टीट्यूड का एक प्रमुख हिस्सा है, जो छात्रों को काफी कठिन लगता है। त्रिकोणमिति गणित की एक प्रमुख शाखा है जो एक त्रिकोण के कोण और लंबाई से संबंधित है. Sin, Cos, Tan, Sec, Cosec, और Cot नाम के कुल 6 त्रिकोणमितीय फंक्शन हैं।इन त्रिकोणमितीय अनुपात के माध्यम से लंबाई और कोण को ज्ञात किया जाता है। त्रिकोणमिति के सभी फार्मूला, ट्रिक्स और प्रश्न इन 6 फंक्शन से सम्बन्धित हैं.
त्रिकोणमिति की परिभाषा (Definition of trigonometry)
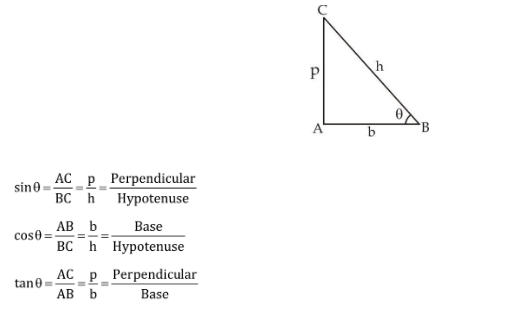
त्रिभुजों और बहुभुजों की भुजाओं की लम्बाई और दो भुजाओं के बीच के कोणों का अध्ययन करने का मुख्य आधार यह है कि समकोण त्रिभुज की किन्ही दो भुजाओं (आधार, लम्ब व कर्ण) का अनुपात उस त्रिभुज के कोणों के मान पर निर्भर करता है। त्रिकोणमिति का ज्यामिति की प्रसिद्ध बौधायन प्रमेय (पाइथागोरस प्रमेय ) से गहरा सम्बन्ध है.
महत्वपूर्ण त्रिकोणमितीय अनुपात की सर्वसमिका (Trigonometry Ratios-Sine, Cosine, Tangent):
त्रिकोणमिति की बेसिक कांसेप्ट पर मजबूत पकड़ के लिए, आपको सभी महत्वपूर्ण त्रिकोणमितीय अनुपात और उनकी सर्वसमिका(आइडेन्टिटी) को जानना चाहिए।
त्रिकोणमितीय अनुपात (Trigonometry Ratios) :
Relations between Trigonometric Ratios
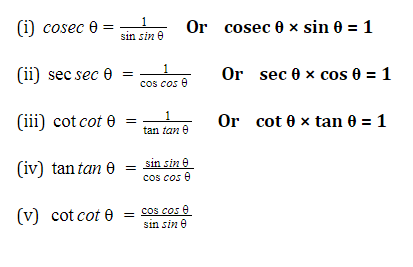
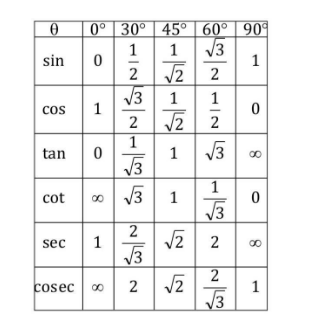
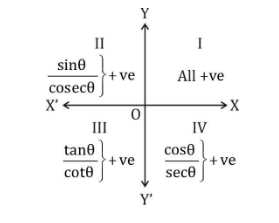
Value of Trigonometric Ratios in Different Quadrants
Different Values of Specific Angle of Trigonometric Ratio
Relation Between Square Of Different Types Of Trigonometric ratios
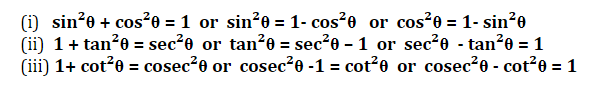
Important Concept to Solve a Specific Type of Question
यदि A + B = 90°
यह हमेशा सत्य होंगे:
(i) sin A. sec B = 1 or sin A = cos B
(ii) cos A. cosec B = 1 or sec A = cosec B
(iii) tan A. tan B = 1 or tan A = cot B
(iv) cot A. cot B = 1
(v) sin²A + sin² B = 1
(vi) cos² A + cos² B = 1
Important Formula for Sum and Difference Of Two Angles
(1) sin (A+B) =sinA. cosB + cosA sinB
(2) sin(A – B) =sinA. cosB – cosA sinB
(3) cos(A+B) =cosA. cosB – sinA sinB
(4) cos(A-B) = cosA. cosB+sinA sinB
(5) 2 sinA.cosB = sin(A+B)+sin (A-B)
(6) 2 cosA. sinB = sin(A+B)-sin (A-B)
(7) 2 sinA. sinB = cos(A-B)-cos(A+B)
(8) 2 cosA.cosB = cos(A+B)+cos(A-B)
(9) sin²A-sin²B = sin(A+B). sin(A-B)
(10) cos²A-cos²B = cos(A+B).cos (A-B)
Different Formula For Tangent

Important Results for Trigonometry
- यदि A + B + C = 180°
तो, tan A + tan B + tan C = tan A. tan B. tan C
- यदि A + B + C = 90°
तो, cot A + cot B + cot C = cot A cot B cot C
- यदि (a) sin θ + cosec θ = 2
तो, ![]()
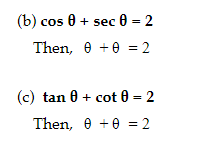
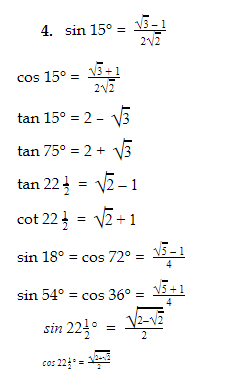
Trigonometry: Maximum & Minimum Value
अधिकतम और न्यूनतम मान
Minimum Maximum
- sin θ, cos θ [odd power] –1 +1
- sin θ, cos θ [even power] 0 +1
- tan θ, cot θ [odd power] –∞ +∞
- tan θ, cot θ [even power] 0 +∞
- sec θ, cosec θ [odd power] –∞ +∞
- sec θ, cosec θ [even power] +1 +∞