Pythagoras Theorem (पाइथागोरस प्रमेय)

इस पोस्ट में Pythagoras Theorem (पाइथागोरस प्रमेय) - परिभाषा, सूत्र और उदाहरण आदि सहित Pythagoras Theorem (पाइथागोरस प्रमेय) की सभी महत्वपूर्ण जानकारी दी हैं.

गणित में पाइथागोरस प्रमेय बहुत ही सामान्य और महत्वपूर्ण विषय. यह समकोण त्रिभुज के विभिन्न पक्षों के बीच के संबंध की व्याख्या करता है. प्रमेय बताता है कि “एक समकोण त्रिभुज में, कर्ण का वर्ग त्रिभुज के अन्य दो पक्षों के वर्गों के योग के बराबर होता है.”

अन्य दो पक्ष यहाँ त्रिभुज के लंबवत और आधार हैं। इसलिए, एक समकोण त्रिभुज में, Hypotenuse इसका सबसे लंबा भाग बन जाता है, क्योंकि यह 90 ° कोण के सामने हैं.

PYTHAGOREAN THEOREM का FORMULA

एक समकोण त्रिभुज में,

A, लंबवत है

B आधार है

C कर्ण है

Therefore, according to the definition of the Pythagorean Theorem, the formula would be:

Hypotenuse²= Perpendicular² + Base²

In other words, it would be:

C²= A²+ B²

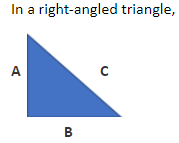
पाइथागोरस प्रमेय का PROOF :

समकोण त्रिभुज में, आधार और लम्ब एक-दूसरे के साथ 90 डिग्री का कोण बनाते हैं. इसलिए, पाइथागोरस प्रमेय के अनुसार, “कर्ण का वर्ग आधार के वर्ग और लंब के वर्ग के योग के बराबर है।”
“the square of the hypotenuse is equal to the sum of a base square and perpendicular square.”

इस प्रमेय को सिद्ध करने के लिए,

मान लें कि एक त्रिभुज ABC है, जिसका कोण B समकोण है.

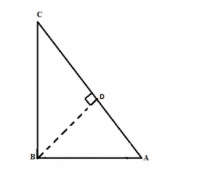
Pythagoras Theorem (पाइथागोरस प्रमेय) – परिभाषा, सूत्र और उदाहरण | Latest Hindi Banking jobs_4.1

हमें सिद्ध करना है : AC²= AB² + BC²

To explain: हम एक सीधा रेखा BD खींचते हैं जो D पर AC से मिलती है.

Proof:

हम प्रमेय द्वारा जानते हैं कि यदि एक समकोण त्रिभुज के कर्ण से समकोण की ओर से खींचा जाता है, तो लम्बवत् के दोनों किनारों पर दो त्रिभुज एक दूसरे के समान होते हैं.

इसलिए,

△ADB ~ △ABC

Hence,

AD/AB = AB/AC (Condition for similarity)

Or, AB² = AD × AC (1)

Also, △BDC ~△ABC (By applying the same theorem)

Therefore,

CD/BC = BC/AC (Condition for similarity)

Or,

BC²= CD × AC (2)

Now,

By adding the equations (1) and (2) we get,

AB² + BC² = AD × AC + CD × AC

AB² + BC² = AC (AD + CD)

Since, AD + CD = AC

Therefore, AC² = AB² + BC²

Hence, the Pythagorean theorem is proved.

APPLICATIONS OF PYTHAGOREAN THEOREM

पाइथागोरस प्रमेय के कुछ अनुप्रयोग

यह जानने के लिए कि त्रिभुज एक समकोण त्रिभुज है या नहीं
एक वर्ग के विकर्ण को खोजने के लिए
समकोण त्रिभुज में, हम किसी भी पक्ष की लंबाई की गणना कर सकते हैं यदि हम अन्य दो पक्षों की लंबाई जानते हैं.

Number Series Questions for Bank Exams

SBI PO Study Plan 2023: SBI PO स्टडी प्लान 2023, देखें प्रीलिम्स की तैयारी के लिए महत्त्वपूर्ण टिप्स | Latest Hindi Banking jobs_90.1

FAQs

Pythagoras Theorem (पाइथागोरस प्रमेय) – परिभाषा, सूत्र और उदाहरण