SBI PO Quantitative Aptitude Quiz
क्वांटिटेटिव एप्टीट्यूड सेक्शन में पूछे गए प्रश्न गणनात्मक और बहुत समय लेने वाले होते हैं। लेकिन एक बार उचित रणनीति, गति और सटीकता के साथ निपटा लेने पर, यह खंड आपको परीक्षा में अधिकतम अंक दिला सकता है। नवीनतम पैटर्न प्रश्नों में से सर्वश्रेष्ठ के साथ अभ्यास करने में आपकी सहायता करने के लिए क्वांटिटेटिव एप्टीट्यूड क्विज़ निम्नलिखित है:
Q1. दो पात्रों में स्प्रिट और पानी का मिश्रण है. पहले पात्र में स्प्रिट का पानी से अनुपात 8 : 3 है और दूसरे पात्र में अनुपात 5 : 1 है. इन पात्रों से 35 लीटर के एक कास्क को भरा जाता है ताकि स्प्रिट और पानी का मिश्रण 4 : 1 के अनुपात में हो सके. पहले पात्र से कितने लीटर निकाला जाता है?
Q2. 2 बोतलों में वाइन, पानी और अल्कोहल का मिश्रण है। पहली बोतल में वाइन, पानी और अल्कोहल के मिश्रण का अनुपात 3 : 5 : 2 है। दूसरी बोतल में पानी और वाइन के मिश्रण का अनुपात 5 : 4 है। पहली बोतल में से 1 लीटर और दूसरी बोतल में से 2 लीटर मिश्रण को मिलाया जाता है। मिश्रण में अल्कोहल का भिन्न ज्ञात कीजिए
Q3. यदि 600 पुरुष एक 5.5 मी चौडी, 4 मीटर गहरी और 405 मी लंबी नहर आधे घंटे में खोद सकते हैं, तो यदि 2500 पुरुष 6 घंटे कार्य करते हुए, 10मी चौड़ी और 8 मीटर गहरी नहर खोदते हैं तो इसकी लंबाई ज्ञात कीजिये?
Q4. सुलेखा और अरुणिमा की आयु क्रमश: 9:8 के अनुपात में है. पांच वर्ष बाद उनकी आयु का अनुपात 10 : 9 होगा. उनकी आयु के मध्य का अंतर ज्ञात कीजिये (वर्ष में)?
Q5. एक व्यक्ति, एक रुकी हुई बस को 18 सेकंड में एक पार करता है। समान बस, एक खम्भे को 4 सेकंड में पार करती है। बस की गति और व्यक्ति की गति का क्रमिक अनुपात कितना है?
Q6. ट्रेन A 52कि.मी/घंटा की गति से यात्रा करते हुए 38कि.मी/घंटे की गति से ट्रेन A की लंबाई के तीन चौथाई की लम्बाई वाली अन्य ट्रेन B को 14 सेकंड में पार करती है. ट्रेन A एक रेलवे प्लेटफार्म से 36सेकंड में गुजरती है. प्लेटफार्म की लम्बाई ज्ञात कीजिये.
Directions (7-10): नीचे प्रत्येक प्रश्न के साथ 3 कथन दिए गए हैं, आपको निर्धारित करना है कि प्रश्न का उत्तर देने के लिए कौन सा कथन आवश्यक है.
Q7. एक ट्रेन पटना से लखनऊ किस समय पहुंचेगी
A. एक ट्रेन विपरीत दिशा में चल रही 97.5 मी की समान लंबाई की अन्य ट्रेन को 9 सेकंड में में पार करती है.
B. ट्रेन पटना से 11:15 पूर्वाहन पर चलती है, जो की 5767कि.मी दूरी पर है.
C. 97.50मी लंबी ट्रेन एक सिग्नल पोल को 5सेकंड में पार करती है.
Q8. एक समभुज त्रिभुज की ऊंचाई ज्ञात कीजिये.
A. त्रिभुज का परिमाप आयात के परिमाप के समान है जिसकी लंबाई और चौड़ाई 5:3 के अनुपात में हैं.
B. वर्ग का परिमाप ज्ञात है, जो कि त्रिभुज के परिमाप के दोगुना है.
C. त्रिभुज का क्षेत्रफल ज्ञात है.
Q9. दो अंक वाली संख्या का मान क्या है?
A. अंकों का योग 5 है.
B. दोनों अकों के वर्गों के मध्य का अंतर 15 है.
C. उनके अंकों का अंतर 3 है.
Q10. एक नाव स्थिर पानी में बिंदु A से B तक यात्रा करने में 2 घंटे का समय लेती है.धरा के प्रतिकूल इसकी गति ज्ञात करने के लिए, निम्नलिखित में से कौन सी जानकारी आवश्यक है?
A. A और B के मध्य की दूरी.
B. B से A तक धारा के अनुकूल लिया गया समय.
C. पानी की धारा की गति.
Directions (11-15): प्रत्येक प्रश्न में दो समीकरण I और II दिए गये हैं. आपको दोनों समीकरणों को हल करना है और उत्तर दीजिये



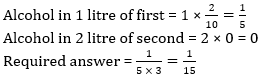

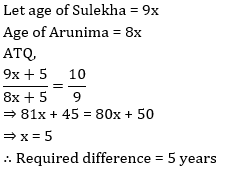





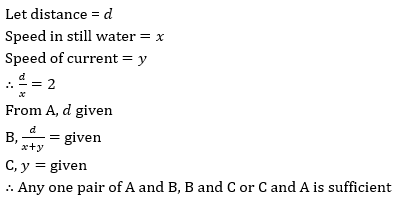
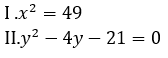
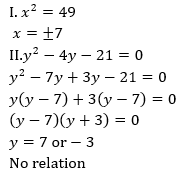
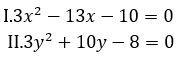
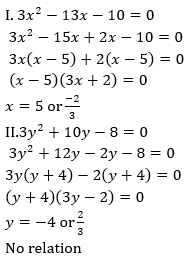
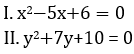
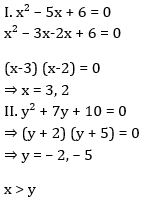
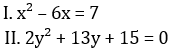
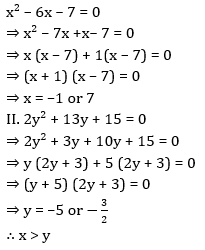
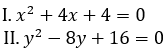
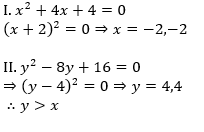



 FCI Phase I क्वांट क्व...
FCI Phase I क्वांट क्व...
 SBI Clerk Prelims क्वांट क...
SBI Clerk Prelims क्वांट क...
 Quantitative Aptitude Quiz For IBPS PO M...
Quantitative Aptitude Quiz For IBPS PO M...

